Downtown Doug Brown

After playing around with a ton of parallel port cards in an attempt to figure out Willem programmer compatibility, I decided it would be useful to write a parallel port tester program. Just a simple utility where you can set the output value of each output pin and read the value of each input pin. Several other test programs exist, but I wasn’t happy with their interfaces, and a lot of them weren’t prepared to easily handle PCI/PCI Express/ExpressCard parallel ports. At worst, they only supported the standard parallel port I/O addresses that new motherboards don’t have anymore. At best, they supported custom parallel ports but required you to manually look up the I/O address range of the card.

Oh, and a lot of the existing tools don’t work with newer versions of Windows. I wanted a tool compatible with newer versions of Windows, both 32-bit and 64-bit.

Introducing Parallel Port Tester:

Simply locate your parallel port in the list that appears in the bottom right. I use several methods to discover parallel ports and their I/O ranges, so you shouldn’t need to enter them manually. If for some reason your port doesn’t show up in the list, you can manually enter the base address of your parallel port (e.g. 0x3000) and hit Enter.

You can toggle parallel port outputs on or off by clicking on the circle representing the pin you want to change. Green represents on (high), black represents off (low). The circles representing input pins are automatically updated while you have the port selected, so you can easily test your inputs. You can also choose whether to use the four control pins as inputs or outputs.

For people who are really interested, I also display the raw register values of the three standard parallel port registers. I show separate values for the control register because what you write to the control register is not guaranteed to be what you read back.

Requirements

Let’s get the requirements out of the way. You will need:

• Windows 2000 or newer. Should work with 2000, XP, Vista, 7, 8, 10, 11, and the various newer server versions. 32- or 64-bit Windows are both supported.
• Microsoft .NET Framework 2.0 or newer

Download

OK, so you’re ready to download it? Here you go.

Download Parallel Port Tester version 1.0.0.2 installer

Special Thanks

Parallel Port Tester includes InpOut32 1.5.0.1 by Phil Gibbons in order to access the parallel ports directly.

Version History

• 1.0: Initial release
• 1.0.0.1: Improves parallel port detection algorithm; previous algorithm was incorrect in certain cases.
• 1.0.0.2: Fixes a bug that was causing a crash for some users.
  • Note: On 1/17/2022, I added an installer for version 1.0.0.2. Prior to this, you needed to manually download and install InpOut32.

Any problems/questions/concerns? Please let me know in the comments below and I’ll try my best to help get you going. Be careful; it might be possible to fry your parallel port if you hook the outputs up wrong. I’m not responsible for any damage done to your computer by using this software.

For sample code that describes how I detect the computer’s parallel ports in Parallel Port Tester, see my blog post: Detecting parallel ports and their I/O addresses in Windows.

Old Installation Instructions

Prior to 1/17/2022, there was no installer, so you had to install the software manually by downloading and installing InpOut32. Nowadays, you can just download the Parallel Port Tester installer and this will all be handled for you automatically. The old installation instructions are preserved below for historical reference:

• Download the old ZIP file of Parallel Port Tester 1.0.0.2 that didn’t use an installer.
• Download InpOut32.dll.
  • Note that I am linking to the best version of InpOut32.dll. It should be compatible with all versions of Windows supported by my program.
• If you are using Windows Vista or newer, you will need to run the InstallDriver.exe program inside the Win32 directory of InpOut32’s distribution in order to install the driver. You only have to do this once, and it’s just so you can get administrator privileges in order to install the driver. Even if you are on a 64-bit operating system, that’s OK. Still run InstallDriver.exe from the Win32 directory.
• Put InpOut32.dll from the Win32 directory into the same directory as ParallelPortTester.exe. Don’t use the x64 directory; that DLL would only be for a 64-bit program, but Parallel Port Tester is not a 64-bit program.

My previous blog posting on this subject from a few years ago sparked quite a bit of interest, so I’d like to follow it up with the latest compatibility information I have. First a quick summary:

Traditional Willem EPROM programmers require your computer to have a parallel port, and almost no computers today have them. You can find add-on parallel port cards, but a good chunk of today’s software is written to work directly with the parallel port addresses that were found on motherboards of older computers (0x378, 0x278, and 0x3BC). Add-on PCI/PCI Express/ExpressCard parallel ports don’t use those addresses.

Unfortunately, the Willem software only lets you pick from a hardcoded list of addresses to work with. The good news, however, is that it does its port access through a DLL called io.dll. There are replacement versions of io.dll that trick the Willem software into talking to a different parallel port address:

• My remapped io.dll (uses TVicPort for port access)
• Ben Ryves’ Remapped io.dll (uses Inpout32 for port access)

It’s actually a good thing that multiple options exist, because sometimes one option works for someone while the other option doesn’t, and vice versa. I would like to list what I have discovered about the various options available in terms of both hardware and software.

Parallel port cards

I have tried a total of four different parallel port cards cards, some of which are hard to find at this time:

• Syba PCI Express 4x serial, 1x parallel card
• Syba ExpressCard 2x serial, 1x parallel card
• Shentek ExpressCard parallel port (hopefully this eBay link sticks around — it’s a Shentek part number 33006 if the link breaks)
• StarTech ExpressCard parallel port

My experience with these is the following. The Syba cards both use Moschip (now ASIX) chipsets, while the Shentek and StarTech cards use Oxford (now PLX Technologies) chipsets.

Both of the ASIX-based cards seem to work fine with no messing around needed. I’ve tested them on my desktop computer with Windows 7 64-bit (my DLL) and my laptop with Windows XP (Ben’s DLL).

The PLX-based cards throw a couple of curveballs into the picture, though. First of all, their bidirectional control pins (strobe, auto/linefeed, initialize, and select printer) do not have pull-up resistors. This causes a problem because they are open-drain/open-collector outputs, so something needs to pull them up when a high value is needed. Otherwise it’s impossible to use them as outputs — and the Willem programmer uses them as outputs. The Willem programmer (mine, at least) doesn’t supply its own pull-ups for those pins either. So in order to gain compatibility with those two cards, you will need to add pull-ups somewhere. To get these cards to work, I manually soldered some 10Kohm pull-up resistors for those lines onto my Willem board. It was a pretty ugly hack, though, so I removed the pull-ups after successfully testing it. Maybe someone can find a cleaner way to do it.

I have no idea about full-size PCI Express or PCI cards that use the PLX chipset. Perhaps they would already have the pull-up resistors in place. I’m just not sure.

The second issue with the PLX cards is described in the “DLLs” section below.

DLLs

The ASIX cards seem to work great with both my DLL and Ben’s DLL, so no further comments are needed here about them.

The Oxford cards don’t behave quite so nicely with my DLL. It seems that TVicPort has trouble reading bytes from odd addresses with the PLX cards, even though it has no such trouble with the ASIX cards. Inpout32 does not have this same issue. I haven’t narrowed down the root problem, but I don’t really care at this point anyway because there’s a fix: if you’re using a PLX chipset, you should use Ben’s DLL instead of mine.

The original reason I made my DLL was because I couldn’t get Ben’s DLL to work correctly with 64-bit Windows 7. It seems that Inpout32 is now 64-bit compatible (and signed), so it may be possible to simply stick with Ben’s DLL. If you plan on going that route, I would recommend downloading the latest version of Inpout32 and grabbing the Inpout32.dll file included with that to go along with Ben’s io.dll. You’ll want to use the 32-bit version even if you’re on a 64-bit operating system. The reason for that is because the Willem software itself is 32-bit. You may need to run the InstallDriver.exe program included with it to get everything to install correctly, but I’m not an expert at Inpout32.

Testing compatibility

If you’d like, you can test your parallel port card with my Parallel Port Tester utility. Make sure all of the outputs and bidirectional pins can correctly output both high and low values. Physically check each pin with a voltmeter while you test. Every card I’ve seen so far outputs 3.3V as a high value. If your bidirectional pins don’t appear to output a high value correctly (or you get weird readbacks in the tester utility), the high value may be floating, thus indicating you need pull-up resistors on those pins. Also make sure the input pins read a high value with nothing attached and a low value when you ground them. It’s OK if the control pins don’t work correctly as inputs; the Willem programmer uses them all as outputs.

Conclusion

The information available in my original post is still very useful and should help walk you through setting up a Willem programmer with various types of cards. I just wanted to share all of my latest compatibility knowledge in a new post because it was all buried in the comments of my original post.

In the early- to mid-1990s, Apple produced their Macintosh Performa line of computers. These computers were meant for home users and typically came bundled with software such as ClarisWorks and Mario Teaches Typing, along with interactive tutorials teaching the basics of how to use the Mac OS. They were sold in places such as Wal-Mart and Sears.

One interesting thing about these computers is that at least initially, they did not come with any software restore disks. If something bad happened and you wiped out your system software (which was easy enough to do — somehow I did it as a kid), you didn’t have a supplied set of disks (or a CD) for restoring the software. Instead, these computers came with software called Apple Backup, and you were supposed to back up your system onto 1.44 MB floppies when you first got it. When you ran Apple Backup, it would let you choose to back up either the full hard drive or just your system folder:

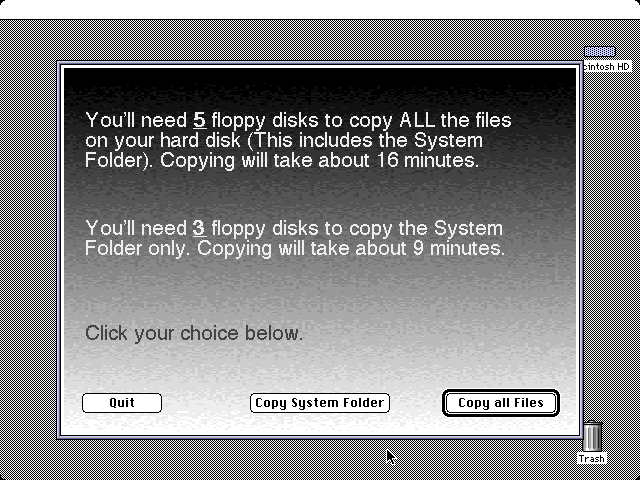
The number of disks needed here is small because I ran it on a simple barebones system to make this screenshot. With all of the bundled software on a stock Performa machine, it would have taken somewhere in the ballpark of 50 floppy disks to complete the backup of the full hard drive. Seriously, how many people would have bothered to buy all of the floppies that would have been necessary, and then actually taken the time to do it? Some people definitely did, and I’m impressed by the dedication. I know my family didn’t bother when I was growing up. It would have been more realistic to only back up user-created files, and then provide a system restore disk (or set of disks) to restore any original software, but the backup software didn’t work that way. Apple obviously learned from their mistake because they began bundling Performa computers with restore CDs at some point later on. (Note: To be completely fair to Apple, it was possible to obtain restore disks from them if you needed to restore your system and your Performa didn’t come with any.)

I ran the backup process on an old Mac for fun, and it guided me through the process of backing up the system. Click the thumbnails to see the full size, if you care:

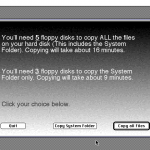
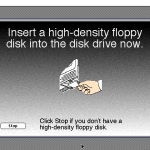
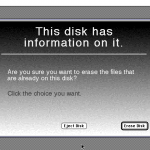
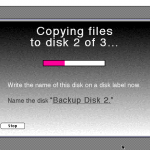
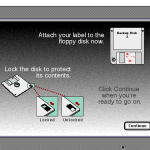
The resulting disks were normal Mac floppy disks, named “Backup Disk 1”, “Backup Disk 2”, and so on, each containing a single 1,414 KB file named Apple Backup Data.

To restore your data after a failure, you would boot up your Performa using the Utilities disk that came with the computer. The Utilities disk contained a barebones system folder along with disk formatting/repair utilities and a program called Apple Restore. You guessed it: Apple Restore was used to restore the system. You would run it and then insert your backup floppies one at a time to restore everything you backed up.

I looked at some of Apple’s later Performa restore CDs, and interestingly enough, they came with programs called “Restore All Software” and “Restore System Software”, each with a folder full of 1,414 KB files named “Data File 1”, “Data File 2”, and so on. So presumably Apple simply used Apple Backup to back up a stock system and stuck the resulting data files onto a CD to create the restore CD.

I decided that it might be useful to have Apple Backup’s file format documented in case someone out there ends up needing to restore files from their old backups (or wants to extract files from a factory restore CD). Although backup floppies from the 90s are probably going bad by now, I think it’s still cool to have the information out there. Anyway, I decided to reverse engineer Apple Backup and one of the factory CD restore programs (which does essentially the same thing as Apple Restore). I believe I have successfully reverse engineered the Apple Backup file format.

The rest of this blog posting contains the technical details about the format of the files that Apple Backup creates.

Overall layout of an Apple Backup data file

• Type code: ‘OBDa’ (CD restore files have type ‘OBDc’ instead, but are otherwise identical in format)
• Creator code: ‘OBBa’
• There is no resource fork, and the data fork content is summarized in the table below:

Backup disk header

Boot blocks

File #1 header

File #1 full path

File #1 data fork data (if any)

File #1 resource fork data (if any)

Zero padding to next multiple of 0x200 bytes

File #2 header

File #2 full path

File #2 data fork data (if any)

File #2 resource fork data (if any)

Zero padding to next multiple of 0x200 bytes

File #3, 4, 5, … until data file is full

Next, allow me to describe the content of the data fork in more detail:

Backup disk header format

All offsets and lengths are in bytes. All multi-byte quantities are in big-endian format as would be expected from a Mac file format.

Offset	Length	Name	Notes
0x00	2	Version	This spec is valid up to and including version 0x0104
0x02	4	Magic number	‘CMWL’ – identifies this file as an Apple Backup file
0x06	2	This disk number	Value is between 1 and the number of disks.
0x08	2	Total number of disks	The total number of disks used for the backup.
0x0A	4	Backup start time	In a Mac time format (seconds since January 1, 1904 00:00:00 local time)
0x0E	4	Backup start time	Appears to always be a duplicate of the value above
0x12	32	Hard drive name	The name of the hard drive that was backed up. Stored as a Pascal-style Str31 (1 byte length, 31 bytes of string data)
0x32	4	Total size of this file	The total size of this restore file; value typically (always?) seen is 0x161800
0x36	4	Total size used in this file	The number of bytes actually used in this restore file; value is typically 0x161800 except on last disk where it is probably going to be smaller.
0x3A	0x1C6	Unused	Filled with zeros

Total length: 0x200 bytes

Boot blocks

These appear to be standard Mac OS boot blocks, 0x400 bytes in size. Easily seen in a hex editor because it begins with LK, and soon thereafter has names: System, Finder, MacsBug, Disassembler, StartUpScreen, Finder, Clipboard. They are written to the hard drive by the restore program when the System Folder is blessed as it’s restored. For just extracting files, they are not really relevant. They begin at an offset of 0x200 from the start of the backup file, and end at an offset of 0x600 (where the first file header begins)

File/folder header format

Each file or folder starts out with a header. Again, all offsets and lengths are in bytes, and everything is big-endian. This header will always begin on a 0x200-byte boundary; padding bytes of zero are added to the end of the previous file’s data fork/resource fork data if needed. The first file header in a backup data file is always at 0x600, immediately after the boot blocks.

Offset	Length	Name	Notes
0x00	2	Version	This spec is valid up to and including version 0x0104
0x02	4	Magic number	‘RLDW’ – identifies this as a file/folder header
0x06	2	Disk number that contains first part of this file/folder	This will match the current disk number, unless this file is split across multiple disks and this is the second, third, etc. part of the file.
0x08	4	Backup start time	Will be the same as the time in the backup disk header
0x0C	4	Offset of header	The offset where this header begins in the disk (example: 0x00000600 in the first file header in every disk)
0x10	32	File/folder name	The name of this file or folder. Stored as a Pascal-style Str31
0x30	2	Which file part this is	1, unless this is part of a file that has been split across multiple disks, in which case it will be 2, 3, etc.
0x32	1	Folder flags	Bit 7 = 1 if this is a folder, 0 if this is a file. Bit 0 = 1 if this is the system folder and it needs to be blessed [selected as the current system folder]
0x33	1	Validity flag	Bit 0 = 1 if the following file info/attributes/dates are valid. Bit 0 = 0 if this was a folder that is known to exist but its properties could not be read during the backup. If a file’s properties cannot be read, the file is skipped during the backup process. So bit 0 = 0 could only happen with folders.
0x34	16	FInfo/DInfo about this file/folder	A standard Mac FInfo or DInfo struct containing info about this file or folder (from HFileInfo or DirInfo)
0x44	16	FXInfo/DXInfo about this file/folder	A standard Mac FXInfo or DXInfo struct containing info about this file or folder (from HFileInfo or DirInfo)
0x54	1	File/folder attributes	Standard ioFlAttrib byte from Mac Toolbox HFileInfo/DirInfo struct
0x55	1	Unused
0x56	4	Creation date	Standard Mac time
0x5A	4	Modification date	Standard Mac time
0x5E	4	Length of file’s data fork	Total length of data fork of the full restored file including all split parts (zero for folders)
0x62	4	Length of file’s resource fork	Total length of resource fork of the full restored file including all split parts (zero for folders)
0x66	4	Length of data fork provided by this disk	The length of data fork data this disk is providing for this file
0x6A	4	Length of resource fork provided by this disk	The length of resource fork data this disk is providing for this file
0x6E	2	Length of full file path	Maximum length of 33*50 (enough space for 50 colon-delimited path elements, with many extra bytes left over). This is the length of the string that immediately follows this header.

Total length: 0x70 bytes. See Inside Macintosh: Files and the Mac Toolbox C headers named “Files.h” and “Finder.h” for more info on FInfo, DInfo, FXInfo, DXInfo, and ioFlAttrib. These items are where the type and creator code, invisible flag, and icon position in folder are stored, for example.

Full path format

The full path is just that: the full path to the folder or file, with the hard drive already being assumed. The components of the path are colon-delimited. The file being restored is the last component of the path. Example:

System Folder:Control Panels:Memory

(if the file being restored is the Memory control panel). It’s just printed as raw bytes, no null terminator or anything — it’s basically a Pascal string with a two-byte length, and the length is at the end of the file/folder header.

The actual file data

Immediately after the full path, the data fork bytes begin (number of bytes = “Length of data fork provided by this disk”), followed by resource fork bytes (number of bytes = “Length of resource fork provided by this disk”). It’s perfectly OK for the length of either (or both) of these to be zero. After that, there is padding (filled with “0” bytes) to the nearest 0x200 byte boundary, and then the next file/folder header begins.

When a file overflows the disk

If there is not enough space remaining on a disk for a complete file (this almost always happens at the end of each data file), the amount of file data that will fit on the disk is stored so that the full disk file size matches the size given in the disk header. Then the first file header on the next disk will be the same file’s header with the exception of the “Which file part this is” field, which will be incremented by one. It is possible for a file’s data to span several disks in this manner; the intermediate disks will only have one file header, followed by a repeat of the file path and data using up all available space on the disk.

For example: Let’s pretend you have 0x1000 bytes remaining on the current data file before its size reaches 1,414 KB. You’re ready to back up a file “Applications:TestApp” that that has a 512 KB data fork and a 128 KB resource fork. The file header will take up 0x70 of those bytes and the full path will take up 20 (0x14) of those bytes, for a total of 0x84 bytes — so there are 0xF7C (3,964) bytes left. So the file header is going to specify a data fork length in this disk of 3,964 bytes, and a resource fork length of 0 on this disk (the total lengths will be filled in as 512 KB and 128 KB though). Then the first 3,964 bytes of the data fork will be written to the file, giving it a total length of 1,414 KB. Then this disk will end. The first file header on the next disk will finish the remaining 520,324 data fork bytes and all of the 131,072 resource fork bytes, and then the next file’s header will begin on the nearest 0x200 byte boundary after that.

Conclusion

As you can see, the format is pretty simple. It’s just basically a disk header followed by a flat list of files until the end of the disk is reached. It should be possible to extract full and partial files from these backup archives even if the data files from some disks are missing. The partial files probably wouldn’t be very useful though.

The original Apple Restore utility didn’t let you pick and choose which files you wanted to restore — it just tried to restore them all, and it would ask you what to do if the file already existed and was newer than the backed up version. I see no reason why a utility couldn’t go through all of these files, give you a list of everything available, and let you selectively extract the files you want. It’s easy to detect what disk a particular backup data file came from because the disk header contains a field for what disk it belongs to.

If anyone’s interested in adding the ability to decode this format in an archive expander program, I would be happy to provide some sample data files. I may or may not decide to write a program to extract files from these backups, depending on how bored I get 🙂

Update 8/23/2022: GitHub user siddhartha77 created a new classic Mac utility called Apple Backup Extractor that can decode this file format. It can even decode what it can from an incomplete set of backup disks. If you’re looking for a way to recover data from these files, this is certainly the way to go!